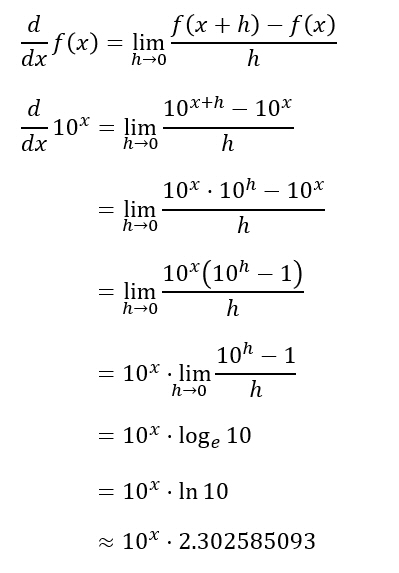371 views
【1】やりたいこと
機械学習では、活性化関数、損失関数、確率分布、学習率減衰、正則化、etc. いろいろな場面で e を使う。
機械学習ライブラリを使わずに、機械学習プログラムを自力実装するためには絶対に必要な知識なので、改めて整理しておきたい。
機械学習ライブラリを使わない Python自力実装シリーズ は以下の通り。
(56) 逆伝播で使う tanh(x)の微分
(57) 逆伝播で使う sigmoid(x)の微分
(58) 逆伝播で使う ReLU(x)の微分
(59) 逆伝播で使う MSE(平均二乗誤差)の微分
(60) 他クラス分類で使う Softmax
(61) 機械学習で多用されるネイピア数とは? ←今回
【2】ネイピア数の定義
(1) 名称
ネイピア数(Napier’s constant)
オイラー数(Euler’s number)
(2) 名称の由来
ネイピア(John Napier)は対数の概念を発明した人物の名前。
ただし、現在の自然対数(底が e の対数)という形での定義・利用は、オイラー(Leonhard Euler) によって体系化された。
→ オイラー数(Euler’s number)とも呼ばれる。
(3) ネイピア数の定義
極限を使った定義:
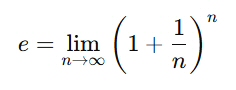
無限級数を使った定義:
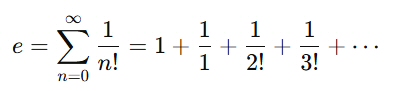
実際に計算された値は?
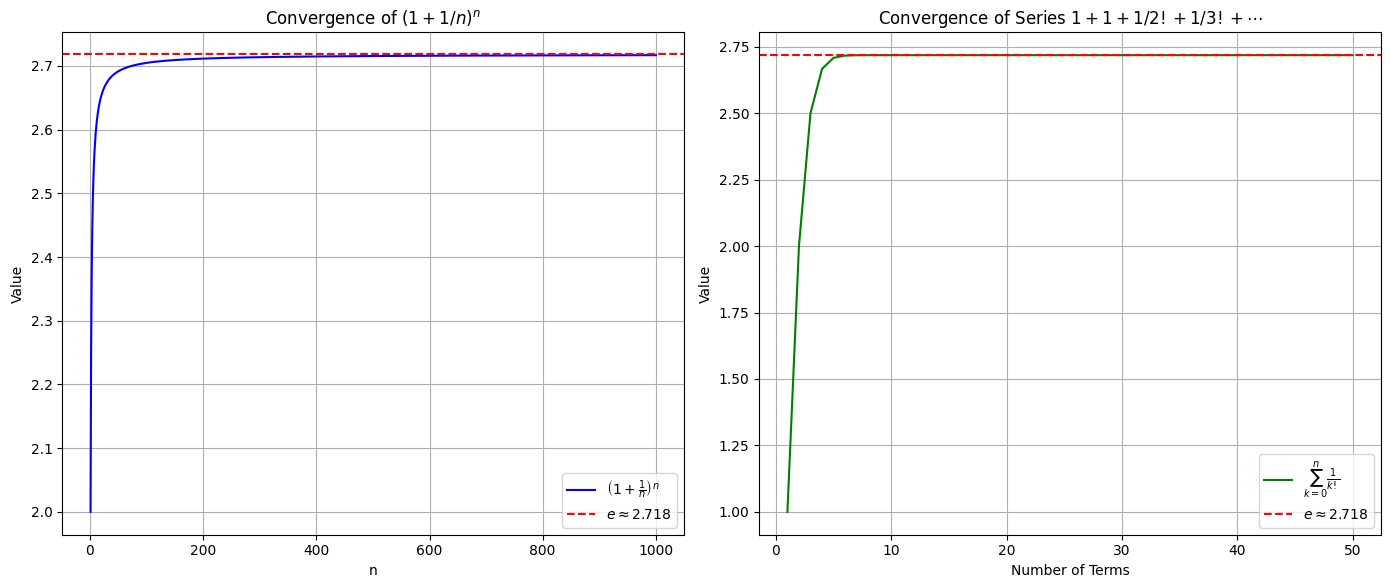
e = 2.718281828459045235360287471352…
この値になることを、収束グラフで視覚化してみる。
どちらの定義式でも n → ∞ のときに e へ収束する様子がよくわかる。
【3】機械学習ではネイピア数 e を多用する。
機械学習では、活性化関数、損失関数、確率分布、学習率減衰、正則化、etc. いろいろな場面で eを使う。
それは・・・
数学的・計算的にとても都合が良いから。
・指数関数と微分の相性が良く(=底がeだと微分した値も同じ)微分がシンプルになる。勾配計算が簡単で安定する。
・指数関数と対数関数が完全に逆関数。Softmax関数 や 交差エントロピー損失関数 において対数・指数の変換が容易。
・Softmax + Cross Entropyの組み合わせでは、指数と対数が打ち消し合って計算が楽になる。
・ロジスティック回帰の損失関数が凸(最小値が1つ)になることが多い。
・確率分布において eは連続的な確率変化を表現するのに向いている。
・学習率減衰(Exponential Decay)で使いやすい。
・正則化(weight decay)も指数関数の性質を活用。L2正則化は eの微分特性があるから簡潔に計算できる。
底が e でなくても機械学習を実現することはできる。
しかし…
例えば、10進数に馴染みがある我々にとってわかりやすそうな 底=10 としてみる。
すると…
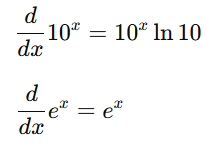
e を使った方がシンプルに記述できるし、計算ロジックも単純になる。
FPUが特殊な回路であった時代は遥か昔、計算速度も問題ない。
【4】eの特徴
| # | 特徴 |
|---|---|
| 1 | 微分しても形が変わらない。 指数関数 ex は微分しても変わらない(学習に便利) |
| 2 | 対数関数と指数関数が完全に逆関数になる。 log(ex) = x なので、計算がシンプル |
| 3 | 成長や確率の変化をなめらかに表現できる |
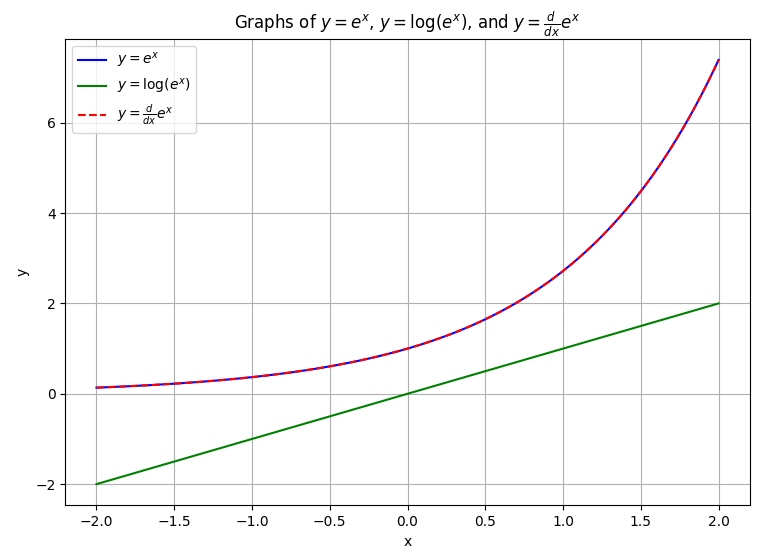
上記の式を 1枚のグラフ上に表示してみる。
ただし、dex/dx = ex なので、この 2式は完全に重なっている。
import numpy as np
import matplotlib.pyplot as plt
# xの範囲を定義
x = np.linspace(-2, 2, 400)
# 各関数の定義
y_exp = np.exp(x) # y = e^x
y_log_exp = np.log(np.exp(x)) # y = log(e^x) → x
y_derivative = np.exp(x) # y = d/dx e^x → e^x
# グラフの描画
plt.figure(figsize=(8, 6))
plt.plot(x, y_exp, label=r'$y = e^x$', color='blue')
plt.plot(x, y_log_exp, label=r'$y = \log(e^x)$', color='green')
plt.plot(x, y_derivative, label=r'$y = \frac{d}{dx}e^x$', color='red', linestyle='--')
plt.title('Graphs of $y = e^x$, $y = \\log(e^x)$, and $y = \\frac{d}{dx}e^x$')
plt.xlabel('x')
plt.ylabel('y')
plt.grid(True)
plt.legend()
plt.show()
【5】「微分しても同じ」を証明する。
1) exの微分は?
(1) 目的
下式を証明したい。
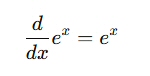
(2) 証明
微分の定義は?
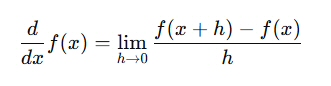
これに f(x) = ex を代入する。
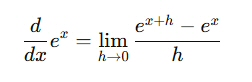 ・・・(1)
・・・(1)
指数法則により、
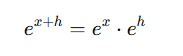
これを (1)に代入する。
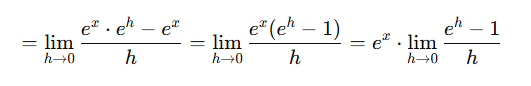 ・・・(2)
・・・(2)
ここで、
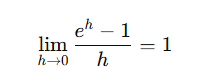 ・・・(3)
・・・(3)
が成立するので、これを (2)に代入すると、
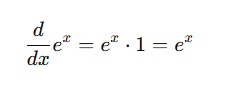
証明できた。
(3) 必要な予備知識
前述の (3) について証明する。
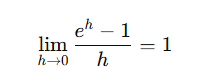
ehをテイラー展開すると、
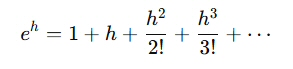
両辺から 1を引き、hで割ると、
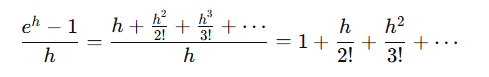
ここで hを 0に近づけると、
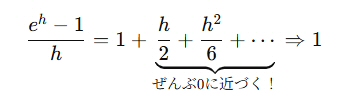
よって、下式が成立する。
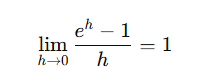
証明できた。
【6】参考
1) 10xの微分
公式を使わずに愚直に展開してみる。